I spent several hours on a new hack, in the end I think it fails my own criteria because I was unable to reduce the variance (chance of loss) despite getting the house edge down as low as 1/216 or 0.4%. I thought to share it here regardless, so you can see my logic, and where it broke down.
The Goal – Get free comps with minimal to zero risk.
Comps are fantastic things, back in January 2013 I wrote a post summarizing my 2012 comps, and the total was about $12,000 for that year, including 3 pretty major vacations. The trouble is that comps are kickbacks based upon what the house plans to win from you, so its a losers game.
The Comp Calculation is simple: Comp Amount = Avergage Bet x Time x House Edge
Another way of looking at this is that it is your Theoretical Loss x comp multiplier (a kickback)
The Gig – colluding to reduce risk of loss
Casino games come in two varieties, those that play against the house, and those that the house delivers on behalf of the players. The former cannot work for this gig, but the latter do, and it comes down to exploiting games with minimal edge to succeed. The candidates were: Roulette, Craps and Baccarat. All three of these games allow you to bet against another person, and all have a different ‘Vig’ (short for Vigorish, aka the Juice, or the house take) roulette is an easy one to explain:
In roulette there are 36 numbers, 18 red, 18 black, and either 1 or 2 zeros (EU wheel has only 1 zero, whereas the American version has 2) If we take the EU version:
- Bob bets $100 on Black
- Dave bets $100 on Red
For 36/37 spins of the wheel, we will have no event for the house, it will take Bobs money to pay Dave, and vice versa. But over time, 1/37 spins should be Zero, and the house wins.
The exploit that exists here from the method of comp calculation. While all casinos run on the same basic premise (along with some discretionary ability) not all kick back at the same ratio. For example, if your theoretical loss (theo) is $100 you may find a top class Casino like the Wynn kicking back $27 whereas a lower end off strip casino kicks you $40.
For Roulette, the 1 in 37 loss rate was too high for me, though the chances are, at 1 spin every 3 minutes that you wouldn’t see a zero until around 45 minutes into the game.
Craps may be the solution -Craps 101
Craps is a game of two halves, and two personalities. The two halves are ‘The Come Out Roll’ and the game proper.
Come out roll: The game starts like this. We are seeking to establish a point number, which can be either 4,5,6,8,9,10. Every number you roll on the come out has an impact. 4,5,6,8,9,10 will result in a point being established (the game proper is now afoot) rolling a 7 or 11 will win on the Pass Line (PL), lose on the Don’t Pass Line (DPL); 2,3 will lose on the PL, and win on the DPL… 12 will lose on the PL and push on the DPL.
2,3 and 12 are called Craps numbers, and 12 is special because it is the house edge.
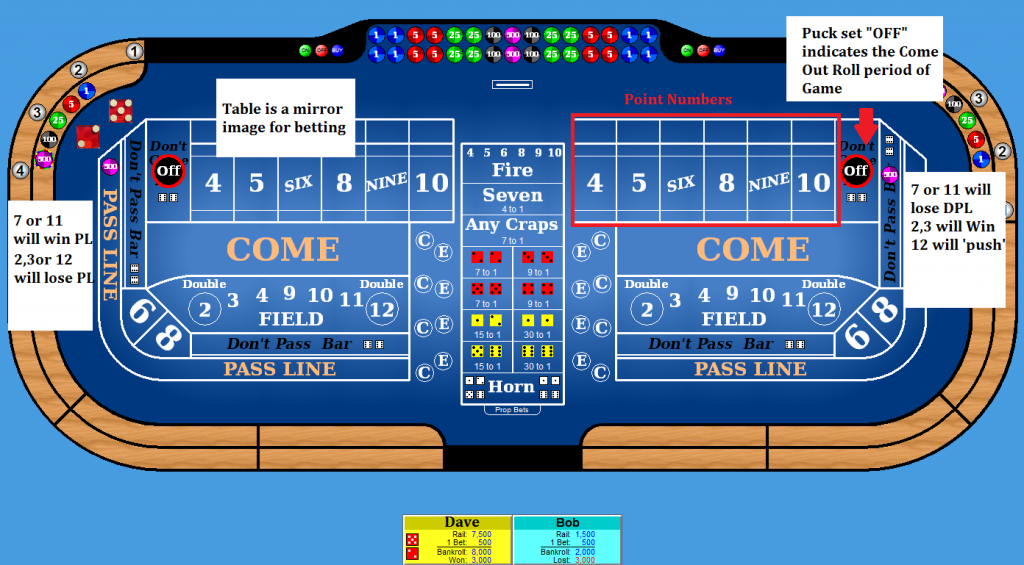
Once we have a point established (a 4,5,6,8,9.10), the Pass Line wins when you roll that number again before a 7 rolls, and loses if the 7 rolls first. The DPL is the exact opposite, losing if the point number repeats before the 7 comes in, and winning if the 7 rolls first.
So that’s the game, two halves (Come Out Roll, and Point Established) and two personalities (PL, and DPL)
It is worth noting that bets behind the PL and DPL are called Odds and are the only bet in the casino with zero edge for the house, however, most casinos will not rate this bet when assigning comps (though they may on discretionary comps from the game supervisor). What this means is that if you were to bet behind the line you could put down any amount, and as long as you had a collaborator to offset this bet, you would have no exposure in the event of a win or loss.
Checking the Math
This is the first time the gig failed. It was late at night and I was lazy, so instead of figuring out the math behind the game outlined above, I just googled ‘pass and don’t pass house edge’ and came across this thread from Wizard of Vegas (the forum attached to Wizard of Odds, a very well respected gaming site) unfortunately thread was started by a guy who didn’t understand the basic premise of probability, but the problem was the answers given were actually incorrect too. At first blush I took them as gospel, but then I did a double take and realized they made no mathematical sense. The comments were, if you play both the PL and DPL simultaneously the house edge becomes the sum of the individual house edges:
- Regular Game PL House Edge = 1.41%
- Regular Game DPL House Edge = 1.36%
That thread stated the house edge of playing both would be 2.77%, which is 1/36 (the same odds as rolling a 12)
However, I thought that this couldn’t be the case, because you don’t lose on a 12 all the time, and you only lose half your money on a 12. Logically speaking, if you had two craps tables side by side, on a regular one and one where you lost all your money (both PL and DPL) on a 12 at any time (regardless of phase of game) they would be different beasts, and the 2.77% is in fact a fallacious number due to this.
I went on to join that forum and start asking questions, I am not a statistician (I did elect Stats in high school, but I also dropped out of high school…) but I have a good eyeball for such things, and now I have the actual number reduced to 0.4% by normalizing the game rules above.
My logic was that in order for you to lose using the PL/DPL gig you need a 12 to roll on the Come Out only, which could be then expressed mathematically as the chances of rolling a 7, then a 12 (not just the chances of rolling a 12) That would be:
1/6 * 1/36 for 1/216 or 0.4%
We have a winner!
The spread here is that if you find a casino that will kick back about 1/3 or more of their Theo, and the Theo for craps is 1.385% (2.77%/2) you could capture comps of 0.46% for a house edge of 0.4%.
While that might sound like a minor spread of 0.06% what you need to consider is that when the house wins it will only take half of your average team bet, but you are being comped on your total average team bet.
- Bob bets $100 PL Theo (loss) for Bob would be 1.41 Comp at 1/3 would be $0.47
- Dave bets $100 DPL Theo (loss)for Dave would be $1.36 Comp at 1/3 would be $0.45
Total comp would be $0.92 for $200, but the expected loss of 0.4 would only impact Bobs play, because Dave can never lose (12 crap is a push, not a loss) so you would actually expect to lose 0.4% of the time, but the impact would be halved. The spread now is a more healthy 0.52.
Why it’s still a failure
I deemed this a failure because of variance. Over infinity, playing a regular game of craps with a 1/216 loss rate you could roll 215 times before the event of a 7 then 12 rolling. However, each “come out roll” has a 1/36 chance of the event occurring. What’s more, statistics are taken over infinity, and there is nothing stopping this theory blowing up by a team entering a dice game and having 10 x 12s roll back to back. The chances of this happening are (1/36 * 1/36) to the power of 10, which is very unlikely, but that isn’t going to make you feel any better if it should happen!
This actually ties into the same fault with stock market returns when people cite an average of X%, as the duration of the investment (or the craps roll) is such as small relative segment and variance is massive.
Conclusion
I hope you enjoyed my failure here. I learned a lot from it, and interestingly enough, by writing up the failure rather than discarding it I actually found a couple of different ‘tricks’ as to how the tables can turn further in your favor, and actually make this a viable strategy. Due to the length I’ll post it as a Part 2, Success! Hacking Comps.
PS – for the statisticians among you, do you see a difference in calculating 7, 12 roll probability with 7 [non point number eg 2,3,7,11] then the 12? I’m wrapping my head around that now.
I find it fascinating that a guy who wants to be a Financial Advisor spends time gambling.
Well, actually I find it helpful for advising. It is simple to say ‘this is bad’ and play the vanilla approach, but that doesn’t indicate understanding of the nuances of the system.
The interesting correlation is that understanding gambling and its psychology allows you to understand flaws within a savings or investment strategy, indeed, they utilize monte carlo sims to find weaknesses in a strategy.
I personally think it is perfectly acceptable for a person to gamble, or to pick single stocks – but I would advise that it is done with a portion of disposable income and that it is manageable. I am not the type of advisor who would say ‘you have to quit gambling to get to retirement goal’. I am the sort who would look at all of your outflows and indicate areas for improvement.
For me, if a person had a net worth of X and was invested in a manner that hedged risk and created sufficient inflows to offset outflows, I wouldn’t mind if they took a few bucks each month an gambled it.
But the real essence of what I am trying to do with these Casino posts is to explore vulnerabilities within programs – they are loyalty programs no different from an an airline or hotel, and while I would personally never mileage run for status, it doesn’t mean I would want to explore it for value purposes.
Looking forward to part 2! I love craps and try to make it to Vegas once a year. Your formula for calculating comps is interesting. Whenever I’ve asked a casino how comps are calculated, I’ve never gotten a straight answer. The pit boss just mumbles something nonsensical.
I find it perfectly acceptable to gamble in moderation as long as someone doesn’t plan on making money from the game itself. If I happen to come out ahead, great. Whatever money I take to Vegas I plan on losing and consider it money from my “entertainment” fund.
Yeah, that is the only way to gamble – it has to be the same as saying you will take X to a fancy restaurant or a ballgame or whatnot – expect to lose everything, and if you should win that should be a surprise.
Though I have to say part 2 does work, its kinda like this in that for gamblers, it might seem a bit boring, since you are really reducing the gambling aspect out and just are racing against the clock to not lose.
My trick to hacking comps has nothing to do with the odds of winning in a certain game. The trick is to make yourself appear as if you are a high roller when you actually gamble very little. There are a few very simple ways to trick casinos into thinking you are a big time gambler.
That’s a valid, but separate discussion, and something I’m bringing in later. These are all facets of the ‘Hack’ and together they work better than separate.
I too like the Wizard of Odds/Vegas both because of the interesting math/statistics problems and the chance to chuckle along with degenerates.
Can you be more specific about this? I can’t imagine that’s much more complicated, given that the events are independent.
I’m trying to get to the statistical root of what makes a losing event.
If you roll any number other than 7 before a 12 you don’t lose on the 12, with the exception of rolling craps/11 EG
7,4,12 (don’t lose)
7,11,12 (lose)
7,7,12 (lose)
7,11,2,3,5,12 (don’t lose)
The point number prior to the 12 means you can’t lose on it.
Also,
7,5,2,3,11,12 (don’t lose) because the point 5 shields the 12 regardless of craps/11 rolling
Did that make any sense???! 🙂
Ahh…. now I understand. There’s a sequence of numbers following 7 (2,3,7,11) that could proceed 12 and trigger a loss.
I have a little baby with a cold, so the quick version. The odds of not establishing a point on the first roll in any sequence is 1/3. The odds of not establishing a point on the first two rolls is 1/9. And so on. Little bit less for the 1/36 odds of a loss. I forget how the different odds are compiled; the odds are easiest to give for any set number of rolls.
Sorry, my brain is taxed for the night.
The more important challenge, I think, is getting a casino to comp both partners who sit at the same craps table making identical inverse bets for however long it takes. Unless one can randomize.
Thanks Harvson! I hope the little one gets well soon- as for the last part, don’t worry about it, I’ve already got that covered 🙂
I’m not sure why you are saying its necessary to roll a 7 before you hit your 12. When you place your bets on both sides the only way that you lose a portion of your bankroll is if the next roll is a 12. If you put $1 on pass and $1 on Don’t Pass and then your roll anything from 2 through 11 you are ultimately breaking even. But when the next roll is a 12 you are only coming away with $1 from your $2 that were wagered. This means there is a 1/36*1/2= 1/72 or 1.389% house edge. I might be missing something in your logic but I believe this should be the house edge.
The long way to do this would be to imagine betting $1 on each side for each of the 36 possible dice rolls. If we do this we would end up betting $72 and we would lose our $1 when the 12 was rolled. 1/72= 1.389% lost to the house.
Because you only lose on 12 when it is a come out roll, which is created by a 7 being rolled. There can be many 12s rolled that would not cause a loss.
So if I understand your strategy, you are assuming that there will be times that you will be placing a bet on both Pass and Don’t pass after the point has already been established(when it is not the come out roll).
But I’m pretty sure the only time you are allowed to place a Don’t pass bet in Craps is on the come out roll. You are allowed to place a Pass bet at any time during the game because if you place a Pass bet after the point has been established the casino is happy to give you even odds that your point will be rolled before a 7. However they will not allow a Don’t Pass bet after the point has been established because that would give the player an advantage. For example if the point was 4, you would have a 2 to 1 advantage on placing a Don’t pass bet hoping that a 7 would be rolled before the 4. The house is not willing to pay you even odds on a bet they know you have the advantage on.
Which brings me back to my original line of thinking. If you cannot bet on both sides after a come out roll then you are left to a strategy where you are only betting both sides on rolls where you are establishing the point. So my initial calculations should be right.
Or I could be misinterpreting everything and missing a finer point of your strategy. I think we both agree that the odds are against us, but figuring out how exactly is always a fun exercise. Where’s the cocktail waitress? Don’t we get comp drinks for discussing this?
You are correct about the don’t pass line must be placed on the come out roll. My point isn’t that I would try to bet after a point was established, it was just that the only way you can lose is on a 12, but not all 12’s will make you lose, because they should roll 1/36 times, but sometimes when they do roll you will be protected from their impact due to their being a point established.
And yes, we certainly need comped drinks to figure this out!
As I was falling asleep last night, I remembered that 7-3-3-12 is also a loss, as is 7-3-4-5-6-3-12.
Look at what the Wizard and co. have done about the so-called “Fire Bet.” I think the best way to get the odds would be to generate a giant random number sequence with entries from 2 to 12, with numbers appearing according to their probabilities, and then sample random sequences, to pull out sequences that begin with 7 and end with 12 and bootstrap the odds.
Sorry. I meant 7-4-4-12 and 7-4-6-5-4-12 and 7-4-4-5-5-12 lose.
Yep – exactly. Fire Bet math might well do it… good thinking!
I’m putting up part 2 now.