If I had a dollar for every article I have seen lauding the magic of compound interest I’d be able to go have a nice steak dinner somewhere. Or I could invest it, and over time, magically become a millionaire. Compound interest really is a fantastic thing, but we need to understand the components, and not get too excited about magic…instead, it is time to take control of things.
Compound Interest is the term given to the growth of money. It has just two components:
- Time and Interest Rate
The longer you save, and the higher the rate of saving, the more money that magically appears.
However, when it comes to actually saving, whether that is for a home, a college fund, or retirement there are three other variables that matter:
- How much you have now (Present Value)
- How much you add to that from your own money (Payment)
- How much you need at the end (Future Value)
Where people go wrong
Firstly, many people don’t have a goal. There is no firm knowledge of what they should be aiming for at the end. This target number seems so far away that many will take the approach of ‘as much as possible’. This leads to all sorts of problems, such as taking on too much risk to earn more, or not taking on enough.
The pretty charts
Let’s say you are 20 years old and your goal is to save $1M by age 50. Most models will suggest something along the lines of:
- Present Value = $0
- Interest Rate 8%
- Time 30 years
- Final Value = $1M
- Payment is… $671 per month
These make really pretty graphs too:
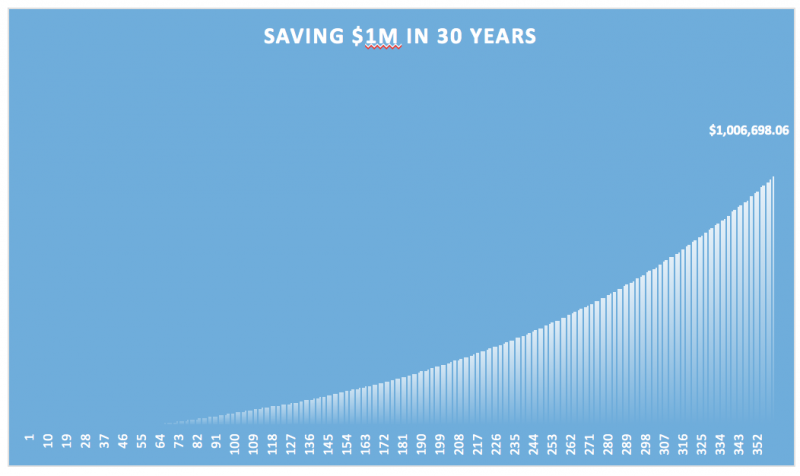
Seems like a little, or like a lot?
Tell me now that if I could save $671 a month for 30 years and I’d have a million and I’d be happy with it, but If I was 20 years old again I’d think you were crazy. In truth, how many people at that age can really afford to set aside that much money for retirement? College expenses and socializing are top of the list of things to worry about, as they should be.
The real danger of this is twofold
A big danger that comes from this is that people put off their retirement savings for too long. However, that is quite fixable. The number you have to adjust in the equation is Payment. If you elect to not save the $671 until you graduate and start saving at age 25 instead, the payment changes as follows:
- Present Value = $0
- Interest Rate 8%
- Time 25 years
- Final Value = $1M
- Payment is… $1051 per month
Seems huge right? But is it really that bad? Think of it this way, if you have graduated and can join a company with a 401(k) match you can use that ‘free money’ to offset the spread between $671 and $1051, and you’re likely to be earning that much more from having a degree. Of course I am assuming you get a job that is….
So while it sounds like a huge deal for the payment to increase so dramatically each month, it needent be. What’s more.. you will likely be earning more money as your career progresses, so you can handle the payments that much more easily, and even increase them.
There will come a time though, when it becomes prohibitively late, and the at is when you have to start changing the $1M by 50 to by age 60… or 70.
The real problem
The biggest problem that I see people make is that they chase Alpha to make up for their shortcomings. Instead of adjusting the savings rate, or the duration of saving, they just change the interest rate. Got no savings by age 27, but only want to save $671 per month, why not adjust the rate of return:
- Present Value = $0
- Interest Rate 12.1%
- Time 23 years
- Final Value = $1M
- Payment is… $671 per month
The problem with this is that in order to get more return, people take on unnecessary amounts of risk, they rely on the market to do too much, and don’t focus on saving enough. While there is magic in compound interest, believing it to be found only in the interest rate when saving is a deadly thing for any plan.
Do you know what your retirement number is, and how much risk you are willing to take in order to add less of your own money into making it happen? A couple of things that might help, you may or may not need a million. And assuming an 8% return from your investments in this low rate environment comes with risk.